Betrachtungen zur Poissonzahl

Autor: Prof. Dipl.-Ing. Johannes Kunz, Institutspartner, IWK Institut für Werkstofftechnik und Kunststoffverarbeitung Rapperswil an der OST Ostschweizer Fachhochschule

Die Poissonzahl, benannt nach dem französischen Physiker und Mathematiker Siméon Denis Poisson (1781-1840), setzt die Verformung eines Körpers quer zur Beanspruchungsrichtung ins Verhältnis zu seiner Längsverformung (Abb. 1). Sie ist für die Berechnungspraktiker ein unverzichtbarer Werkstoffkennwert – gleichbedeutend wie der Elastizitäts- bzw. Kriechmodul.

Blick in Datenbanken und Fachliteratur

Leider aber – aus Sicht der Anwendungstechnik – wird die Poissonzahl noch immer nicht systematisch gemessen und fehlt dementsprechend in den meisten Datenbanken. Im Campus-Grundwertekatalog, der auf DIN EN ISO 10350-1 [1] basiert, ist die Poissonzahl nicht enthalten. In der Datenbank MatWeb [2] gibt es für die Poissonzahl immerhin eine Rubrik; Zahlenangaben findet man aber unter den fast 98’000 Polymerwerkstoffen nur gerade bei gut 1700 davon. Warum das so ist, bleibe dahingestellt.

Erschwerend für den Anwender kommt dazu, dass die wenigen in der Fachliteratur auffindbaren Zahlenwerte der Poissonzahl z.T. weit auseinander klaffen. Wenn dann etwa behauptet wird, Abweichungen der verwendeten Poissonzahl-Werte würden sich auf die Berechnungsergebnisse nur minim auswirken, so ist dies weder hilfreich noch generell zutreffend. Insbesondere bei Verformungsberechnungen ist je nach Problemstellung mit Einflüssen in der Grössenordnung von bis zu mehreren 10 Prozent zu rechnen. Wird beispielsweise bei der Berechnung des dünnwandigen Zylinders unter Innendruck die Poissonzahl von 0,35 auf 0,4 erhöht, reduziert sich die Umfangsdehnung um rund 3 Prozent, die Längsdehnung dagegen um über 30 Prozent.

Unzutreffend und theoretisch nicht begründbar sind auch Aussagen, die Grösse der Poissonzahl bewege sich bei realen Werkstoffen zwischen 0,3 und 0,5, wobei der untere Wert die Grenze linear-elastischen Verhaltens markiere. Es gibt isotrope Werkstoffe mit linear-elastischem Verhalten und Poissonzahlen um 0,2 oder darunter, wie z.B. technische Gläser [3].

Beim kritischen Blick in die Fachliteratur fragt man sich auch, warum die international genormte Bezeichnung „Poissonzahl“ oder allenfalls „Querkontraktionszahl“ und das Symbol „“ nicht durchwegs verwendet werden [4]. So begegnet man nach wie vor dem Symbol „“ sowie Begriffen wie Querzahl, Querdehnzahl oder auch Poissonsche Konstante, welch letzteres sie wegen ihrer diversen Abhängigkeiten definitiv nicht ist.

Definitionen und Bezeichnungen

Für die nachfolgenden Erörterungen ist es wichtig, die unterschiedlichen Definitionen der Poissonzahl auseinanderzuhalten und mit geeigneten Indizes zu kennzeichnen.

Werden die Dehnungen technisch bestimmt, d.h. als Längenänderung bezogen auf die zugehörige Ausgangslänge, so gilt bei Isotropie und mit den Richtungsbezeichnungen von Abb. 1 die Beziehung

(1)

als technische Poissonzahl. Sie kann noch von diversen Einflussgrössen wie Temperatur, Höhe, Dauer und Geschwindigkeit der Beanspruchung, Kristallisationsgrad usw. abhängen.

Bei Berechnungen mit wahren, differenziellen Dehnungen, z.B. bei FEM-Analysen mit grossen Verformungen, ist konsequenterweise die wahre Poissonzahl

(2)

zu verwenden. Merklich wird ihre Abweichung von der technischen Poissonzahl ab etwa 5 % technischer Dehnung . In (2) ist die technische Poissonzahl  in ihrer Abhängigkeit von der technischen Dehnung einzusetzen, wie das weiter unten mit Beziehung (9) erläutert wird.

Die dehnungsabhängigen Poissonzahlen nach (1) und (2) nehmen bei verschwindend kleinen Dehnungen übereinstimmend den Wert  an. Dieser kann zur klaren Unterscheidung als Basis-Poissonzahl bezeichnet werden. Er lässt sich für den praktischen Gebrauch mit der Poissonzahl gleichsetzen, die aus dem Kurzzeit-Zugversuch [4] bei Raumtemperatur hervorgeht.

Poissonzahl und Steifigkeit

Interessant ist die Erkenntnis, dass sich die Poissonzahl umso mehr dem Wert 0,5 nähert, je geringer der Elastizitätsmodul ist [5, 6]. Diese qualitative Aussage scheint nicht nur auf Kunststoffe zuzutreffen, sondern grundsätzlich auch auf metallische Konstruktionswerkstoffe. Bei näherer Betrachtung von unverstärkten bzw. ungefüllten Thermoplasten zeigt sich tatsächlich ein Zusammenhang zwischen den Grössenordnungen der Steifigkeit, repräsentiert durch den Kurzzeit-Zugmodul  bei Raumtemperatur, und der Basis-Poissonzahl  (Abb. 2). Diese Tatsache kann für die Ableitung einer Formel genutzt werden, mit der sich die Basis-Poissonzahl abschätzen lässt gemäss

(3)

Darin ist  der Bezugs-E-Modul. Dabei muss mit einer Unschärfe von etwa  gerechnet werden. Eine allfällige Abweichung von der Raumtemperatur  als Bezugsgrösse wie auch der Einfluss der Belastungsdauer können mit einer weiteren, früher schon publizierten Näherungsformel berücksichtigt werden [7]. Deren Kombination mit (3) führt zur Beziehung

(4)

mit  als Kriechmodul zur Zeit  und  als aktueller Temperatur.

Die wenigen konkret bekannten Zahlenwerte deuten darauf hin, dass auch bei verstärkten und gefüllten Thermoplasten die Poissonzahl mit zunehmender Steifigkeit sinkt. Zur Ableitung einer Näherungsformel reicht aber die vorhandene Datenbasis nicht aus. Immerhin kann pro 10 Gewichts-Prozenten Verstärkungs- bzw. Füllstoff von einer Abnahme der Poissonzahl um etwa 0,01 ausgegangen werden.

So hilfreich solche Näherungen sein können, so darf man sich nicht darüber hinwegtäuschen, dass sie nicht mehr sein können und wollen als ein Behelf bei Fehlen genauerer Angaben. Aussagen über ihre Trefflichkeit im Einzelfall sind ohnehin nicht möglich. Dennoch hat ihre Verwendung gegenüber einer gefühlsmässigen Daumenpeilung zumindest den Vorteil, dass die Festlegung der Poissonzahl nachvollziehbar ist und dokumentiert werden kann.

Poissonzahl und Kompressibilität

In der Poissonzahl drückt sich auch die Komprimierbarkeit eines Werkstoffs aus, also dessen Eigenschaft, unter mechanischer Belastung sein Volumen zu ändern. Allerdings ist die Skala bei der Poissonzahl etwas ungewöhnlich. Bei isotropen Werkstoffen reicht sie von  bei maximaler Kompressibilität bis  bei deren Fehlen. Darin nicht enthalten ist der Sonderfall des auxetisches Verhaltens [8] mit negativer Poissonzahl, wie es z.B. bei hochverstrecktem PTFE auftreten kann.

Ein logischer Kennwert für die Kompressibilität lässt sich aus der Volumendehnung ableiten. Die technische Volumendehnung, also die auf das Ausgangsvolumen  bezogene Volumenänderung , ist bei kleinen Dehnungen und linear-viskoelastischem, isotropem Werkstoffverhalten bestimmt durch die Summe der linearen Dehnungen in den drei kartesischen Hauptrichtungen (Abb. 1). Bei beliebigem mehrachsigem Spannungszustand mit  ergibt sich als technische Volumendehnung

(5)

unter Verwendung des natürlichen Mehrachsigkeitsgrades [9] gemäss

(6)

Das eigentliche technische Kompressibilitätsmass wird in (5) durch den Klammerausdruck

(7)

dargestellt. Dessen Skala reicht von  bei Volumenkonstanz bis  bei maximaler Kompressibilität. Diese technische Kompressibilität  ist mit dem Elastizitätsmodul  wesentlich mitbestimmend für den Kompressionsmodul

(8)

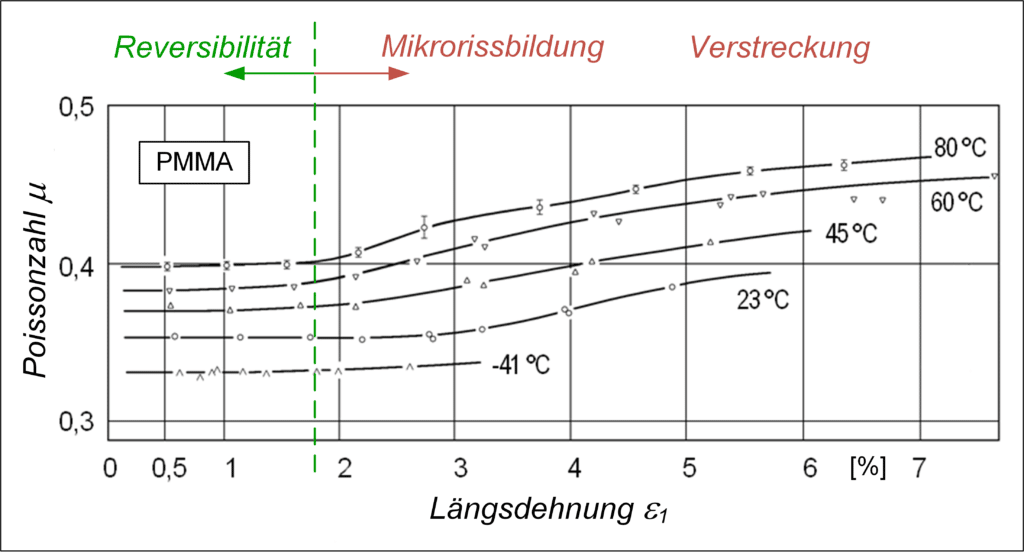
Wie die Erfahrung zeigt, nimmt die Kompressibilität mit zunehmender Verformung eines Werkstoffs ab, bis er beim allfälligen Übergang zum plastischen Verhalten inkompressibel wird. Dies bestätigt sich auch in der Zunahme der Poissonzahl in Funktion der Dehnung, und zwar sowohl in der technischen Definition als auch in ihrer wahren Grösse (Abb. 3).

Nun könnte man auch versuchen, die Kompressibilität als wahre Grösse zu bestimmen. Dies ist aber in Anbetracht der obigen Erkenntnisse ein komplexes Unterfangen. Damit wird man sich für die Beurteilung der Kompressibilität aus praktischen Gründen auf die einfache, technisch basierte Beziehung (7) stützen.

Dehnungsabhängigkeit

Den prägnantesten Einfluss auf die Poissonzahl hat zweifellos die Temperatur. Mit zunehmender Erweichung sinkt die Kompressibilität, d.h. die Poissonzahl strebt ihrer oberen Grenze zu [10 – 12]. Weniger bekannt ist, dass sie – wie oben erläutert – auch von der Dehnung abhängt. Dieser Einfluss ist aber nicht zu unterschätzen. Er macht sich vor allem bei grösseren Verformungen bemerkbar, wobei sich zwei unterschiedliche Phänomene überlagern.

In erster Linie sind es strukturelle Veränderungen, die sich bei Dehnungen oberhalb des schädigungsfreien, reversiblen Verformungsbereiches einstellen und die Poissonzahl ansteigen lassen [11, 12] (Abb. 3). Sie betreffen die Konformation der Makromoleküle und den Ordnungszustand des Gefüges. Als Begründung hierfür wird die Zunahme von grossräumigen Platzwechseln des Hauptdispersionsgebietes während einer Verformung angeführt, mit der ein starker Anstieg der Querkontraktionszahl zu volumenkonstanter Verformung verbunden ist. Diese Änderung erfolgt nach Frank [11] erst, „wenn die volumenkonstanten visko-elastischen Verformungsanteile eine gewisse Grösse erreicht haben und sich ein viskoser Verformungsanteil bemerkbar macht.“ Oder anders ausgedrückt: Im reversiblen, schädigungsfreien Verformungsbereich ist die Poissonzahl mehr oder weniger konstant, ab einer werkstoffcharakteristischen Grenzdehnung [13, 14] steigt sie bei abnehmender Kompressibilität kontinuierlich an. Duktile Werkstoffe sind im vollplastischen Zustand inkompressibel.

Der zweite Effekt ist rein geometrischer Art. Denn grössere Dehnungen bewirken geometrisch bedingt eine gewisse Abnahme der Poissonzahl, was sich vor allem bei der technischen Poissonzahl  bemerkbar macht. Dies mag etwas erstaunen, lässt sich aber anhand einer einfachen Überlegung zeigen. Bei einachsigem Spannungszustand berechnet man unter der Annahme konstanter Volumendehnung für die technische Poissonzahl in Funktion der technischen Dehnung  die Beziehung

(9)

mit  als Basis-Poissonzahl für verschwindend kleine Dehnungen. Da bei vollplastischem, inkompressiblem Verhalten  ist, vereinfacht sich (8) zum Ausdruck [15]

(10)

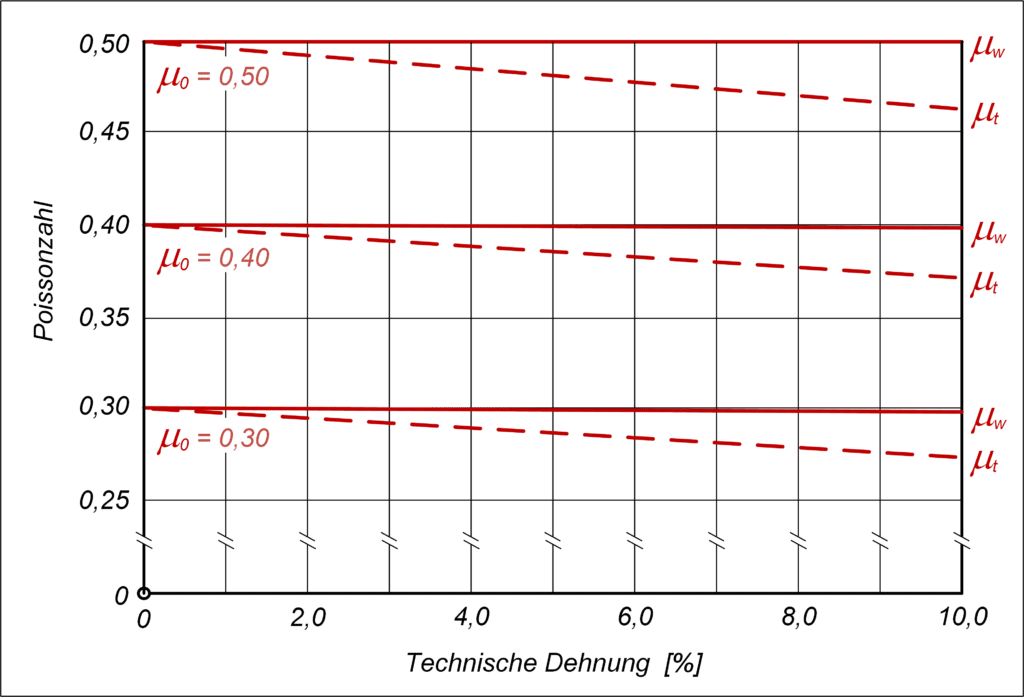
Beim Grenzübergang  führt (10) zum Wert , und bei  beträgt die technische Poissonzahl für Inkompressibilität noch  (Abb. 4). Setzt man (10) in die Beziehung (2) für die wahre Poissonzahl ein, so zeigt sich, dass auch diese mit wachsender Dehnung abnimmt. Nur gerade bei Inkompressibilität ist sie mit  konstant (Abb. 4).

Generell gilt: Bei Berechnungsproblemen mit grossen Verformungen und Verwendung der wahren Poissonzahl (2) ist deren Dehnungsabhängigkeit durch Beachtung von (9) zu berücksichtigen. Dazu kann auch der Berechnungsansatz von Dassow [12] hilfreich sein. Mit diesem können gemessene Werte der wahren Poissonzahl funktionalisiert werden, und zwar zu einem sigmoidförmigen Ausdruck (Abb. 5) in der Form

(11)

Die Grössen  und  stammen aus der Poissonzahl-Messung,  und  sind charakteristische Werte aus dem gleichzeitig aufgenommenen Spannungs-Dehnungs-Diagramm. Bei Erreichen des vollplastischen Zustandes mit Inkompressibilität müsste theoretisch  sein. Der Ansatz hat allerdings den Nachteil, dass er die Existenz einer Streckgrenze voraussetzt (Abb. 5).

In diesem Zusammenhang von Bedeutung ist aber auch die Tatsache, dass sich eine anfänglich vorhandene Isotropie wegen dem Einfluss der Dehnung auf die Poissonzahl zur Orthotropie wandelt, wie man dies bei grossen Verformungen in einer Richtung auch in Bezug auf die Festigkeiten kennt. Damit wird das Querdehnungsverhalten in den drei Hauptebenen des Spannungszustandes unterschiedlich, und es gibt keine gemeinsame Poissonzahl mehr. Doch wegen der mit grösseren Dehnungen zunehmenden Nichtlinearität können die elastizitätstheoretischen Gesetze der Orthotropie streng genommen nicht angewendet werden. In der Praxis liegt der Ausweg aus dieser Komplexität meistens darin, dass man dennoch näherungsweise von isotropem Verhalten ausgeht.

Schlussbemerkung

Der sachgerechte Umgang mit der an sich unspektakulären Poissonzahl erfordert gründliche Kenntnisse über ihre Eigenheiten und über das Querkontraktionsverhalten der Werkstoffe. Dies gilt speziell bei der Auslegung von Bauteilen, die grösseren Verformungen unterworfen sind. Dringend wünschbar wäre die Verfügbarkeit verlässlichen Zahlenmaterials, ansonsten läuft jede Bemühung um realitätsnahe Berechnungsresultate mittels noch so ausgefeilter Programme letztlich ins Leere. Über die nach wie vor unbefriedigende Datenbasis können auch die verschiedenen Abschätzformeln nicht hinwegtäuschen, auch wenn sie als Behelf dienlich sein mögen. Es ist an den Anwendern, ihre diesbezüglichen Ansprüche bei Kunststofferzeugern, Datenbankbetreibern, Herstellern und Ausrüstern von Prüfmaschinen usw. geltend zu machen. Einer systematischen Messung und Dokumentation der Poissonzahl sollte im Zeitalter der berührungslosen Zugprüfung z.B. mittels Videoextensometrie eigentlich nichts im Wege stehen.

Literatur

   [1]  DIN EN ISO 10350-1:2018: Kunststoffe – Ermittlung und Darstellung vergleichbarer Einpunktkennwerte – Teil 1: Formmassen

   [2]  MatWeb. Material Property Data. Online-Datenbank www.matweb.com

   [3]  Wikipedia: Poissonzahl; abgerufen 9.1.2023

   [4]  DIN EN ISO 527-1:2019-12: Kunststoffe – Bestimmung der Zugeigenschaften – Teil 1: Allgemeine Grundsätze

   [5]  Oberbach, K.: Kunststoff-Kennwerte für Konstrukteure. 2. Aufl., Carl Hanser Verlag München 1980, S. 104

   [6]  Meyer, B.-R.: Entwicklung und Konstruktion von Kunststoffteilen. Carl Hanser Verlag München 2021, S. 140

   [7]  Kunz, J.: Die Querkontraktionszahl in der Konstruktionspraxis. KunststoffXtra 1(2011)6, S. 27-30

   [8]  Wikipedia: Auxetisches Material, abgerufen 9.1.2023

   [9]  Kunz, J.: Spannungszustand und Werkstoffverhalten. KunststoffXtra 8(2018)4, S. 14-18

[10]  Schenkel, G.: Verfahren zum Bestimmen der Poissonzahl insbesondere bei Kunststoffen. Kunststoffe 63(1973)1, S. 49-53

[11]  Frank, U.: Die Querkontraktionszahl von Kunststoffen, dargestellt am Beispiel amorpher Thermoplaste. Diss. Universität Stuttgart 1984

[12]  Dassow, J.: Messung und Beschreibung der Querkontraktionszahl von teilkristallinen Thermoplasten als nichtlinear viskoelastischer Materialkennwert. Diss. RWTH Aachen 1996; Aachener Beiträge zur Kunststoffverarbeitung, Band 50, 1996

[13]  Kunz, J.: Reversibilität als Auslegungskriterium. Kunststoffe 108(2018)2, S. 67-71

[14]  Kunz, J.: Ein Plädoyer für die dehnungsbezogene Auslegung. Kunststoffe 101(2011)4, S. 50-54

[15]  Pózfalvi, Ö.: Über das Elastizitätsgesetz und die Poissonsche Zahl von gummielastischen Werkstoffen. Periodica Polytechnica; Transportation Engineering 10(1982)1, S. 61-66